CNN Architecture Dig Deeper
CNN Architecture Dig Deeper
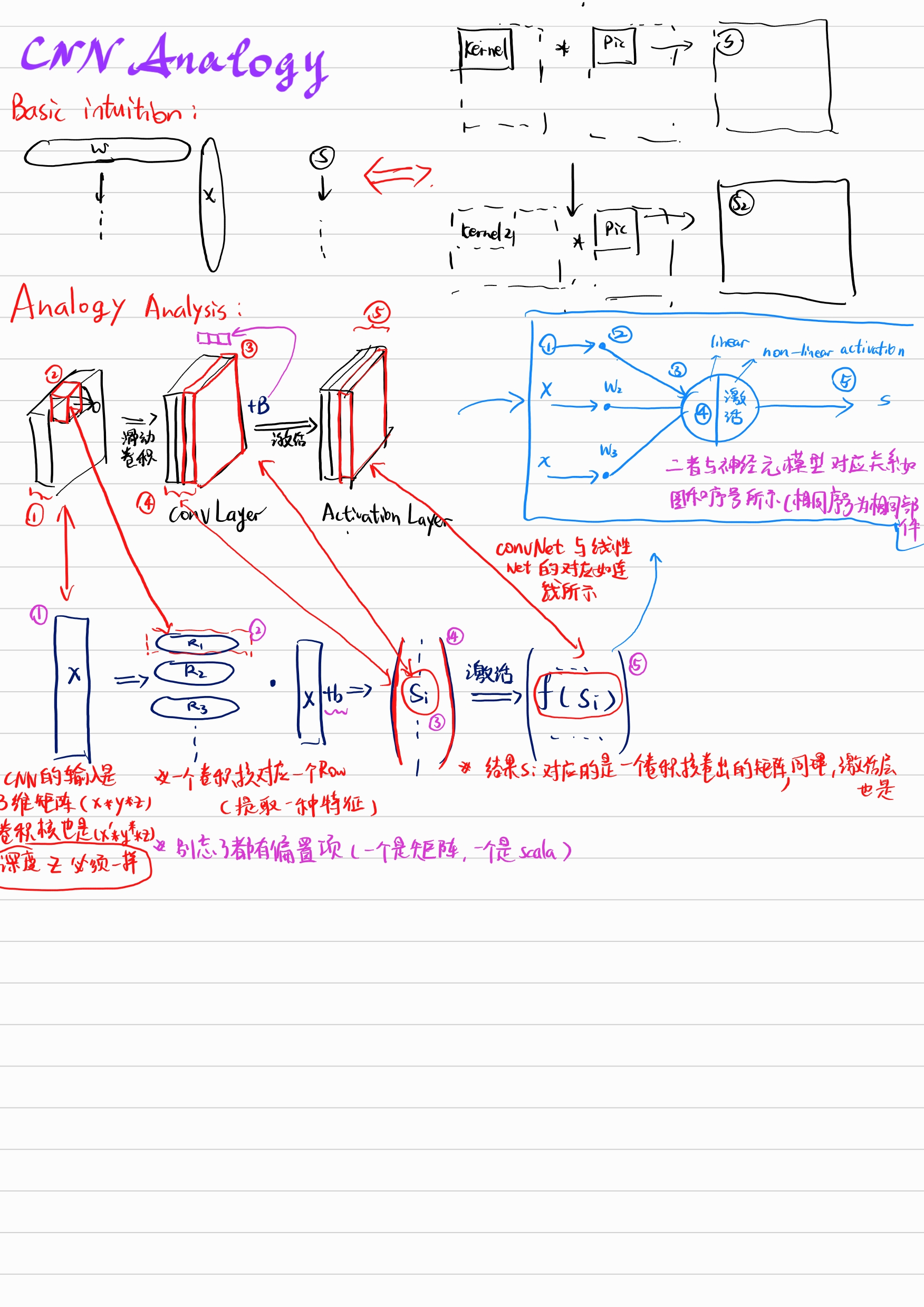
Analogy to the fully connected layer and a single neuron
Convolution Layers
Dimensional description of CNN
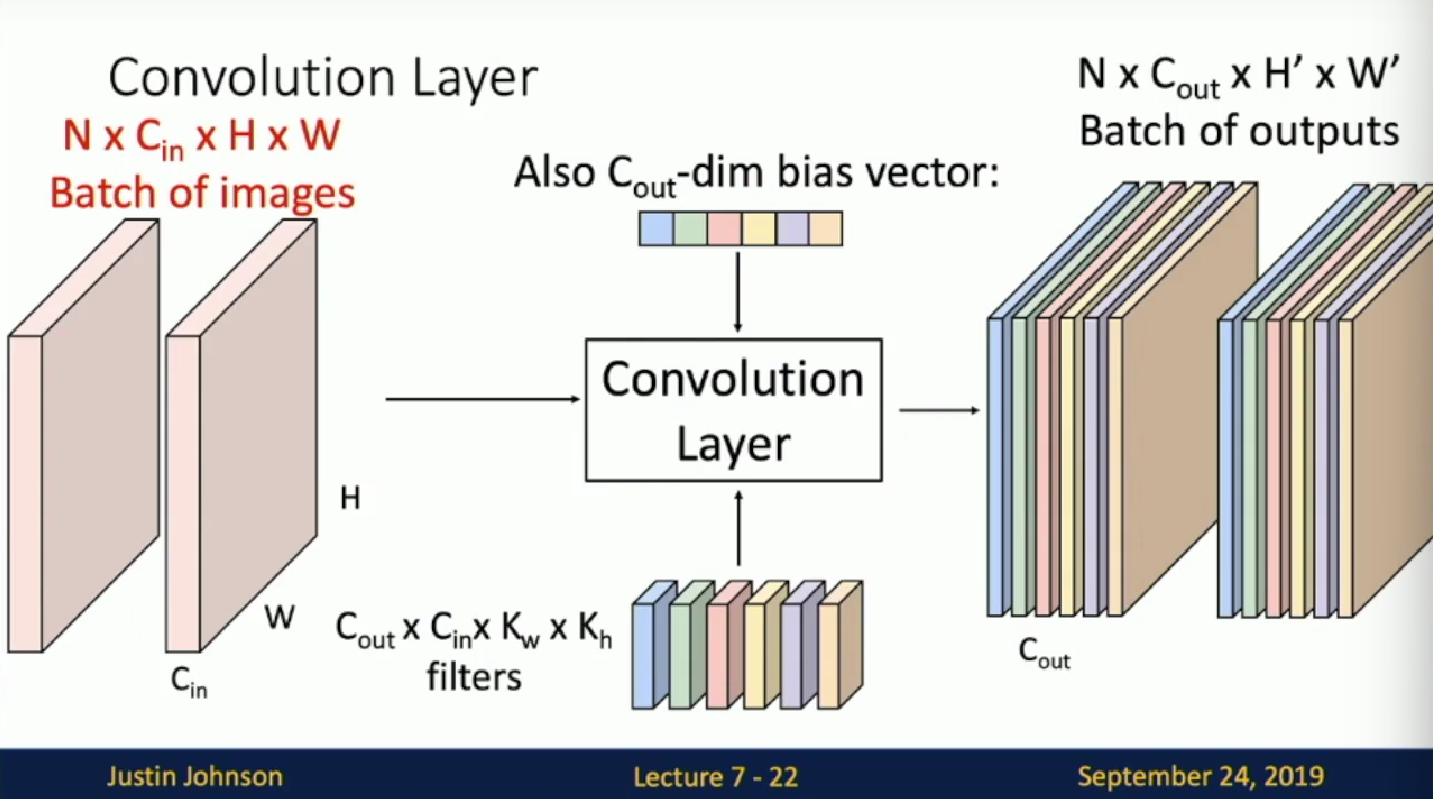
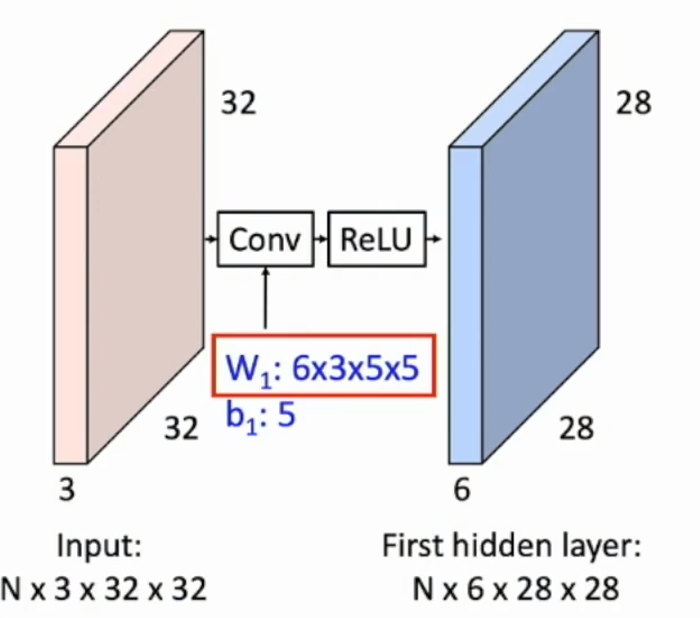
:warning: Notice that we have a batch number of N in practice. So the input is usually of 4-dim.
Stacking of layers
Conv + ReLU connects the layers together
Receptive Fields
For convolution layers, each kernels allow us to see a particular local feature with size in the input equals to the kernels size. So a 3x3 kernel can only see the feature of the local feature with size 3x3 on the original input.
But as we stack convolutional layers together, the complexation helps local features contains richer information, and till one day, the local feature in a deep layer convolution layer will see the feature information from the whole original input picture.
The detailed formular of how the receptive fields grown is given below, as well as its growth visualization

Therefore we get an intuition: bigger receptive fields == deeper network , which is not a health way of improvement. We can use down sampling to shrink the image size namely increase the density of each new outputs’ reception field (imagine we output a 1x1 pixel immediately, then its receptive field instantly reaches full picture. But that is not a multi classifier meant to do)
This is one way of thinking why we need down-sampling layer, and we dig deeper into it later.
Common Patterns

Cheat sheets!
Down Sampling Layer
We introduce max pooling layer and 1x1 convolution layer here. Here is the brief introduction:
1x1 Conv Layer
Apart from the description above, an interesting perspective on 1x1 Conv Layer is that it is actually like a fully connected layer operating on the depth dimension.
Each filter is like a class or column vector of matrix W in FC layers. And the number of filters correspond to the number of W’s columns. Then each filter operates on the input picture independently, just like W’s columns multiply input matrix X independently in columns.
Therefore we can actually build FC networks inside CNN architectures. We can stack 1x1 layer + ReLU Layer several times which acts like a FC networks.
But still 1x1 conv layer is more used in down sampling and adapting the number of depth channel.
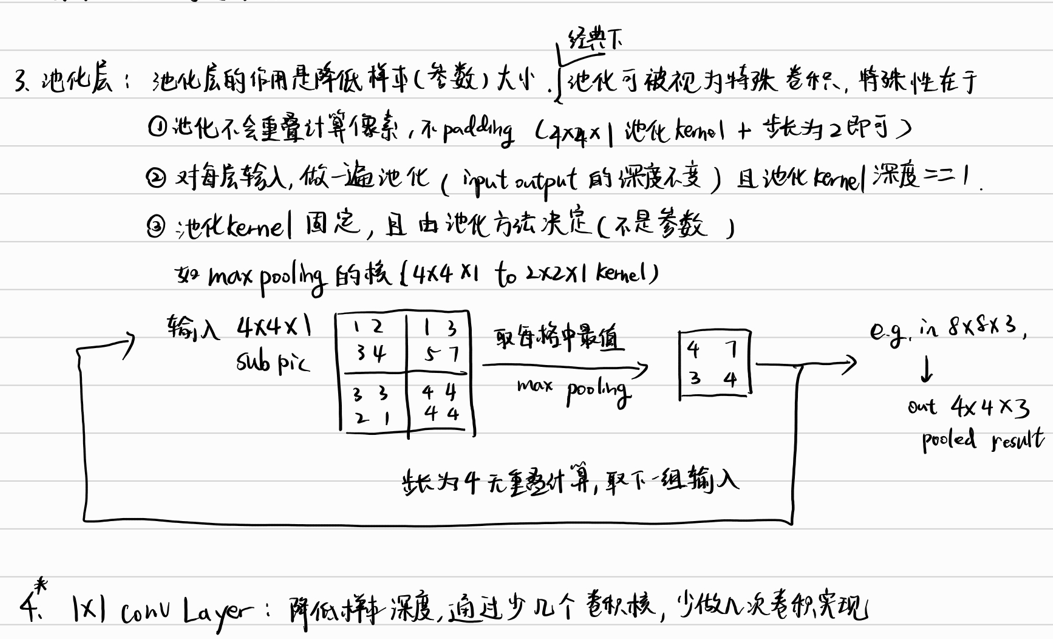
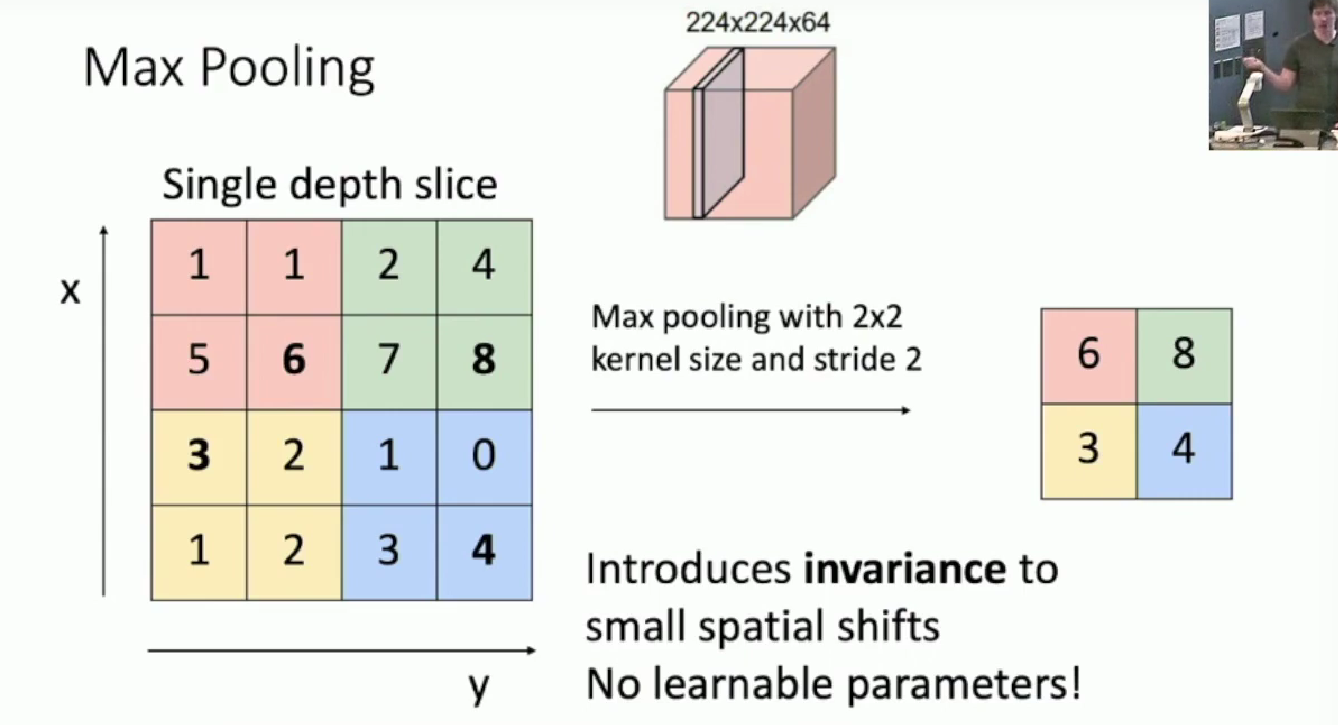
Pooling Layers
The method of pooling is not restricted to max pooling, but the general pattern should be same, like we operate on a single feature slice in depth once at a time, and we downsize the length/height of the picture by pooling function, and like stride equals kernel size.

Sandwiching them!
Conv + Pooling + ReLU is very often used, but deep network is very hard to train! We need normalization to help convergence and help train a deeper network.
Batch Normalization (BN Layer)
General idea: control each layer output to be of zero mean and 1 variance.
BN over FC layers
About how batch normalization function in FC layers. We just perform BN along each feature across all batch dimension.
Normalization across the batch

Learning the shift and bias
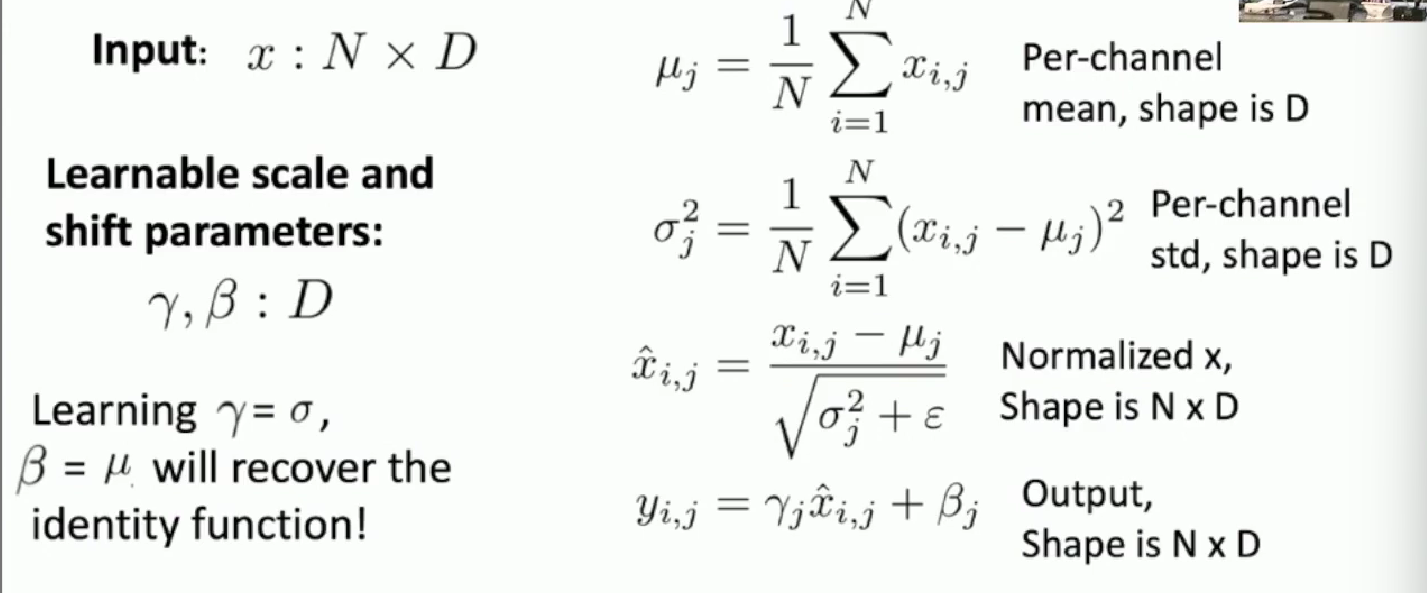
Recover sample independence in test time.
At training time, we do running sum over all $\mu$ and $\sigma$ for each train. The difference is that in test time, the batch dimension vanishes, and if we had done something that relies on the batch dimension in training time, it creates a difference between them. In BN we just do a similar way without using batch dimension in test time, which is the starting sentence of this block.
BN over conv layers

In conv layer, the $\mu$ and $\sigma$ are now vectors of length equals to depth, which is similar to what a bias vector look like!
We can also say, for each depth dim, we consider all pixels in height, length, and across all pictures in a batch to compute the $\mu$ and $\sigma$ .
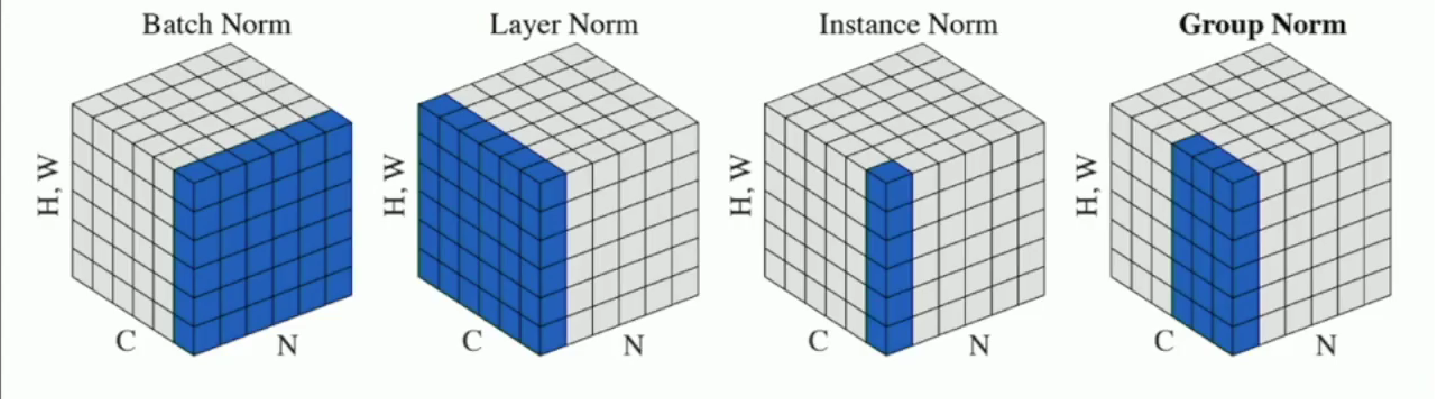
*Layer Normalization
To deal with the incompatibility during test time and training time, we normalize over feature dimension,(for each sample in batch, we consider every pixels in length, height, and channels)
This is common in Recurrent Neuron Network and Transformers.
*Instance Normalization
Similarly, we just do normalization on only length and height dimension namely for each sample in batch and for each channel(feature) in a sample we do sone normalization.