The gradient of functions in linear classifiers in backprop
多维情况下的梯度
多维情况下的梯度是比较棘手的问题,其对应的数学知识是向量值函数。
本文中分析的输入输出的维度格式为:X = (num,dim) , W = (dim, class) , Y = (num, class)
其现实含义是将 num 个 dim 维样本,乘以矩阵 W,即将每个横向量样本通过一个 W 的列向量评分线性函数 $x_i * w_i + b =s_{ic_i}$ ,得到该样本在该类上的评分 $s_{ic_i}$ .
如果将一个输出 y 中的横向量看作是 $f_i$ 则其只和对应的横向量 $x_i$ 有关。对于每个 $f = (f_1,f_2, f_3 \dots , f_{class})$ ,以及 $f_{c_i} = f(x_{i1}, x_{i2}, \dots , x_{in}) = x_i * w_{c_i} + b$ , 其梯度都将会是一个矩阵 w.T, 每个元素是 $\frac{df_i}{dx_ij}$ 。但是我们还有 num 个类似的 $x_i$ 横向量, 此时就有 num 个 w.T, 这是一个四维的张量. 出了一些问题(详见下解答)
然而结论没有错,矩阵和矩阵求导,是四维张量, 如同降一维的向量 $f_i$ 和 $x_i$ 求导是二维矩阵 w.T 一样.
幸运的是,在深度学习中,最终的损失函数对每个 x_i,得出的值是一个标量 $L_i$ , 因此独立考虑每个 $f_i$, 其和对应的 $L_i$ 求导的维数将是一个横向量,num 个堆叠后正好是矩阵的形式
当然也会有其他的方法使得最终导数总是矩阵, 这里也只是分析了对 x 求导的方法,但是结论总是可求导,且导数矩阵和原数据矩阵形状相同.
同时将 x 拆成 num 个独立样本,或拆成 dim 个独立的特征,从而得到对应 num 个 y,dim 个 y 的方法,可以被广泛使用
SVM - Hinge loss gradient

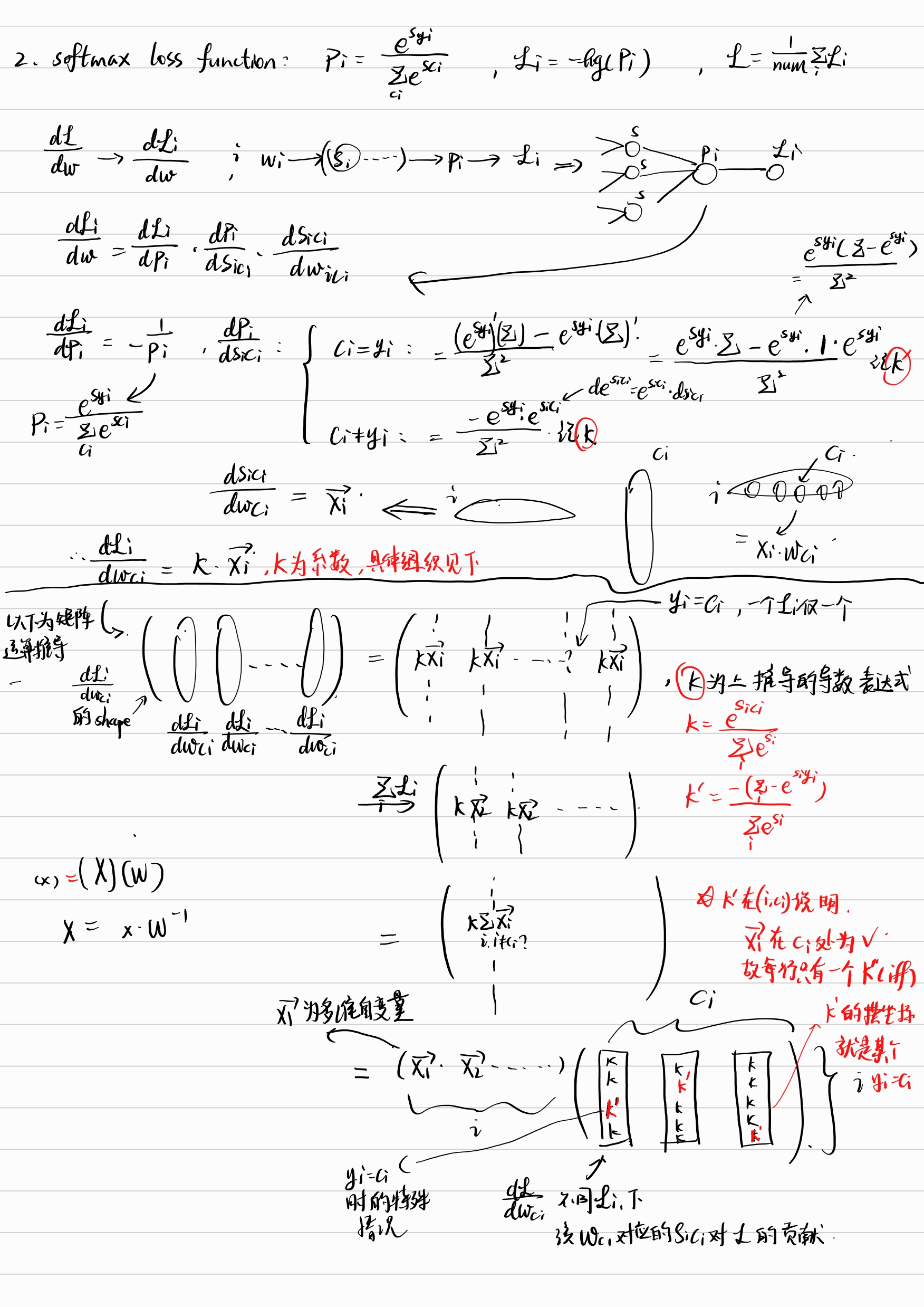
Softmax loss gradient
Fully-connected Layer gradient



Relu layer gradient
类似relu函数的各激活函数的梯度具有相似的性质, 因为激活函数都是 1d to 1d 的标量函数, 因此直接对输入做 element-wise 运算即可, 即做element-wise 的chain-rule 和梯度计算. 因此代码中也不需要用到矩阵乘法.

Other activation function gradient









